Các phương pháp đơn giản để chứng minh 2 đường thẳng song song

Khái Niệm Cơ Bản Về Đường Thẳng Song Song

Để bắt đầu, hãy cùng tìm hiểu những khái niệm cơ bản liên quan đến đường thẳng song song. Từ định nghĩa, tính chất đến các ký hiệu thông dụng, tất cả đều góp phần vào việc hình thành kiến thức nền tảng vững chắc.

Định Nghĩa Đường Thẳng Song Song

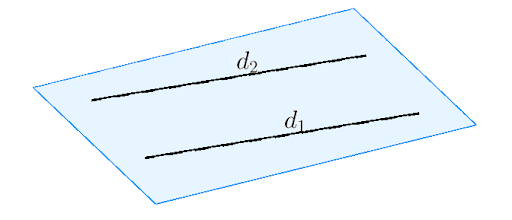
Đường thẳng song song được định nghĩa là hai đường thẳng không bao giờ giao nhau, bất kể kéo dài chúng ra đâu. Đây là một đặc điểm nổi bật mà mọi người thường nhận diện ngay từ cái nhìn đầu tiên. Đường thẳng song song luôn duy trì khoảng cách cố định giữa chúng, điều này tạo nên sự đồng nhất trong không gian hai chiều hoặc ba chiều.

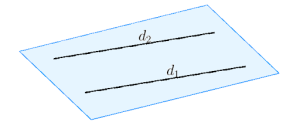
Ví dụ, nếu bạn tưởng tượng hai đường ray của một chiếc tàu, bạn sẽ thấy rằng chúng luôn ở khoảng cách cố định với nhau, và không bao giờ chạm nhau dù cho chiếc tàu có đi nhanh hay chậm đến đâu. Điều này chính là đặc điểm cơ bản của đường thẳng song song.

Tính Chất Của Đường Thẳng Song Song

Một số tính chất quan trọng của đường thẳng song song bao gồm:

• Khoảng cách cố định: Như đã đề cập, khoảng cách giữa hai đường thẳng song song luôn giữ nguyên không thay đổi.
• Góc với đường thẳng cắt: Nếu một đường thẳng cắt hai đường thẳng song song, thì các góc đồng vị sẽ bằng nhau, và các góc so le trong cũng sẽ bằng nhau. Điều này rất hữu ích trong việc chứng minh hai đường thẳng song song.
• Tính chất phản xạ: Mọi điểm trên một đường thẳng song song đều có thể phản ánh chính xác qua đường thẳng còn lại.

Các tính chất này không chỉ giúp chúng ta nhận diện đường thẳng song song mà còn là công cụ quan trọng trong việc chứng minh và giải quyết các bài toán hình học phức tạp.

Các Ký Hiệu Thông Dụng Trong Hình Học

Trong hình học, để diễn đạt mối quan hệ giữa các đường thẳng, các ký hiệu được sử dụng thường xuyên. Một số ký hiệu phổ biến bao gồm:

• Ký hiệu “//” được dùng để biểu thị hai đường thẳng song song.
• Ký hiệu “∠” được dùng để biểu thị các góc giữa các đường thẳng.

Việc nắm rõ các ký hiệu này không chỉ giúp bạn dễ dàng ghi nhớ mà còn hỗ trợ bạn trong quá trình làm bài tập và giao tiếp với người khác về vấn đề liên quan đến hình học.

Phương Pháp Chứng Minh Hai Đường Thẳng Song Song

Có nhiều phương pháp để chứng minh hai đường thẳng song song. Chúng ta sẽ cùng xem xét ba phương pháp chính: sử dụng góc so le trong, góc đồng nhau và tính chất góc trong tam giác.

Sử Dụng Góc So Le Trong

Góc so le trong là một trong những công cụ hữu ích nhất khi chứng minh hai đường thẳng song song. Khi một đường thẳng cắt hai đường thẳng khác, góc so le trong sẽ có những tính chất đặc biệt.

Khi xem xét các góc so le trong, nếu hai góc này bằng nhau, điều đó tức là hai đường thẳng cắt nhau sẽ là hai đường thẳng song song. Đây là một cách đơn giản nhưng hiệu quả để chứng minh tính song song giữa các đường thẳng.

Điều này có thể được chứng minh bằng cách sử dụng định lý Euclide, nơi nhấn mạnh vai trò của các góc trong không gian hình học. Bạn có thể tưởng tượng một tình huống thực tế, như hai con đường trong thành phố không bao giờ gặp nhau, và góc giữa chúng luôn được duy trì giống nhau.

Sử Dụng Góc Đồng Nhau

Góc đồng nhau cũng là một công cụ chứng minh hữu dụng không kém. Hai góc đồng nhau được hình thành khi cùng nằm ở phía đối diện của đường thẳng cắt.

Nếu hai góc này bằng nhau, chúng ta có thể kết luận rằng hai đường thẳng là song song. Việc nhận biết và tính toán các góc đồng nhau thường đòi hỏi sự tinh tế và kỹ năng quan sát tốt.

Chú ý rằng, không phải lúc nào góc đồng nhau cũng dễ nhận biết, đôi khi cần phải kết hợp thêm các yếu tố khác để có thể chứng minh được.

Sử Dụng Tính Chất Góc Trong Tam Giác

Khía cạnh thứ ba trong việc chứng minh hai đường thẳng song song là tính chất góc trong tam giác. Đặc điểm này đặc biệt hữu ích khi làm việc với các hình tam giác, vì nó liên quan đến tổng các góc trong tam giác luôn bằng 180 độ.

Khi có một tam giác và bạn biết được hai góc của nó, bạn có thể dễ dàng tính toán góc còn lại. Nếu góc còn lại này tương ứng với một trong hai góc đã đề cập trước đó, bạn có thể đi đến kết luận rằng hai đường thẳng song song.

Cách tiếp cận này không chỉ mang lại sự chính xác trong tính toán mà còn giúp bạn củng cố thêm kiến thức về góc trong tam giác, mở rộng khả năng tư duy hình học.

Ví Dụ Minh Họa

Để giúp bạn hiểu rõ hơn về các phương pháp chứng minh hai đường thẳng song song, chúng ta sẽ cùng xem xét một số ví dụ minh họa cụ thể.

Ví Dụ 1: Chứng Minh Hai Đường Thẳng Song Song Qua Góc So Le

Giả sử chúng ta có hai đường thẳng a và b, cùng một đường thẳng c cắt chúng tại một điểm. Giả sử góc A (góc so le trong) và góc B (góc so le trong) tạo ra bởi đường thẳng c và hai đường thẳng a, b đảm bảo rằng A = B.

Dựa trên tính chất của góc so le trong, ta có thể kết luận rằng đường thẳng a // đường thẳng b. Đó là một minh chứng rõ ràng và trực quan về mối quan hệ giữa các đường thẳng.

Ví Dụ 2: Chứng Minh Hai Đường Thẳng Song Song Qua Góc Đồng Nhau

Tiếp theo, hãy xem xét hai đường thẳng p và q bị cắt bởi một đường thẳng r. Giả sử góc X và góc Y là hai góc đồng nhau được hình thành bởi đường thẳng r.

Nếu góc X = góc Y, điều này chứng minh rằng đường thẳng p // đường thẳng q. Phương pháp này dễ dàng áp dụng và rất có giá trị trong nhiều trường hợp thực tế.

Ví Dụ 3: Áp Dụng Tính Chất Góc Trong Tam Giác

Cuối cùng, chúng ta sẽ thảo luận về việc áp dụng tính chất góc trong tam giác. Giả sử chúng ta có một tam giác ABC, với các góc A, B, C lần lượt.

Nếu góc A + góc B = 90 độ, điều này dẫn đến góc C sẽ bằng 90 độ. Nếu một đường thẳng đi qua điểm C và cắt đường thẳng AB, bạn có thể áp dụng tính chất của góc để chứng minh rằng các đường thẳng là song song.

Ứng Dụng Của Đường Thẳng Song Song Trong Toán Học

Đường thẳng song song không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn trong toán học và cuộc sống hàng ngày.

Ứng Dụng Trong Giải Bài Tập Hình Học

Khi giải các bài tập hình học, việc nhận diện và chứng minh đường thẳng song song giúp giảm thiểu thời gian và tăng tính chính xác. Nhiều bài toán yêu cầu bạn phải sử dụng tính chất song song để tính toán các góc và đo đạc khoảng cách.

Một bài toán thường gặp trong hình học là tìm góc giữa hai đường thẳng song song và một đường thẳng cắt. Việc áp dụng đúng các phương pháp chứng minh sẽ giúp bạn giải quyết nhanh chóng và hiệu quả.

Ứng Dụng Trong Thiết Kế Kiến Trúc

Trong thiết kế kiến trúc, đường thẳng song song đóng vai trò vô cùng quan trọng. Nó không chỉ giúp tạo nên sự cân đối và hài hòa trong các thiết kế mà còn đảm bảo tính an toàn và ổn định cho các công trình.

Nhà thiết kế sử dụng tính chất của đường thẳng song song để xác định các cấu trúc chính xác, từ đó tạo ra các công trình kiến trúc đẹp mắt và bền vững.

Ứng Dụng Trong Vật Lý

Trong lĩnh vực vật lý, các khái niệm về đường thẳng song song cũng xuất hiện nhiều. Ví dụ, khi nói về lực tác động trên một vật thể, bạn có thể hình dung chúng trong không gian ba chiều, nơi các đường thẳng song song đại diện cho các lực tương tác.

Hiểu rõ về các đường thẳng song song sẽ giúp bạn phân tích và dự đoán hành vi của các vật thể trong không gian một cách chính xác hơn.

Những Lưu Ý Khi Chứng Minh Đường Thẳng Song Song

Khi tiến hành chứng minh hai đường thẳng song song, có một số lưu ý quan trọng mà bạn cần chú ý để tránh những sai sót không đáng có.

Các Sai Lầm Thường Gặp

Một trong những sai lầm phổ biến nhất khi chứng minh đường thẳng song song là nhầm lẫn giữa các loại góc. Ví dụ, khó khăn trong việc xác định góc so le trong và góc đồng nhau có thể dẫn đến kết luận sai.

Ngoài ra, việc không tuân thủ các định lý cơ bản trong hình học cũng sẽ ảnh hưởng đến kết quả của bạn. Do đó, việc nắm vững các định lý và tính chất là vô cùng cần thiết.

Cách Khắc Phục Những Sai Lầm

Để khắc phục những sai lầm này, bạn cần phải rèn luyện kỹ năng quan sát và phân tích. Hãy luôn kiểm tra lại từng bước trong quá trình chứng minh, và so sánh với các định lý đã học.

Thực hành với nhiều bài tập khác nhau cũng sẽ giúp bạn trở nên dạn dĩ hơn và nâng cao khả năng nhận diện và chứng minh đường thẳng song song.

Tầm Quan Trọng Của Việc Chứng Minh Chính Xác

Việc chứng minh chính xác đường thẳng song song không chỉ có ý nghĩa trong toán học mà còn có vai trò quan trọng trong nhiều lĩnh vực khác. Tính chính xác trong chứng minh giúp bạn xây dựng nền tảng kiến thức vững chắc, từ đó tự tin hơn khi tham gia vào các hoạt động liên quan.

Chứng minh 2 đường thẳng song song là một chủ đề phong phú và đa dạng trong hình học. Từ các khái niệm cơ bản đến ứng dụng thực tế, việc hiểu rõ và vận dụng đúng các phương pháp chứng minh sẽ giúp bạn phát triển khả năng tư duy sáng tạo và phân tích.

Hãy luôn duy trì tinh thần tìm tòi, học hỏi để không ngừng mở rộng kiến thức và ứng dụng vào những lĩnh vực mà bạn đang quan tâm.